Torsion of a curve
Definition
If in the context given by curvature of a curve we take
$$ B:=T\times N $$we can define
$$ \tau:=-N\cdot B', $$a quantity that measures the speed of rotation of $B$, or "how the plane that theoretically contain the curve is changing with time".
Visualization
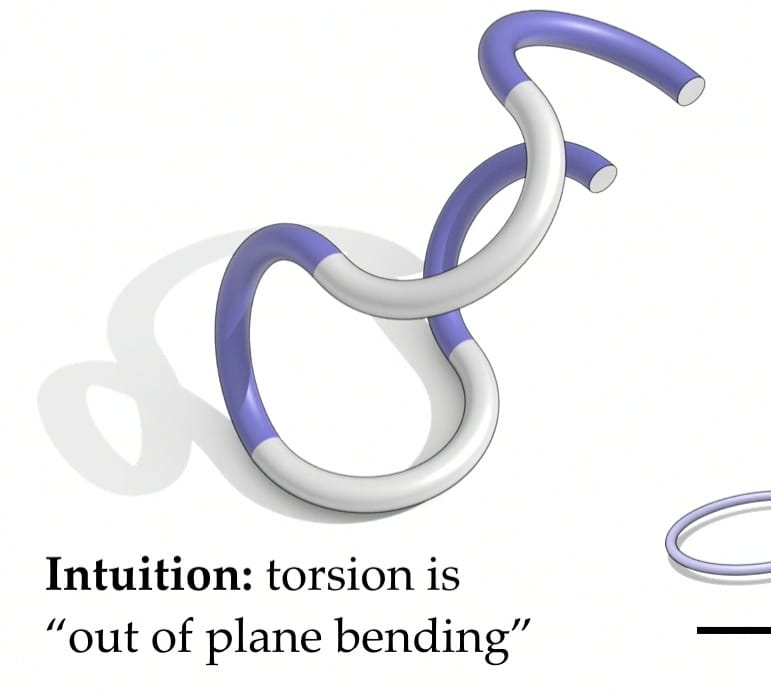
A way to visualize the torsion, in addition to the curvature of a curve:
The curvature is how much I deform a tiny ring segment and the torsion is how much I twist when joining two ring segments. Put another way, locally (when zoomed in enough), a curve can look like a "chunk" of a ring (not necessarily of angle $\pi$ like the ones in the picture) to which we attach another chunk of a ring. The torsion is how much we twist when joining the two rings.
________________________________________
________________________________________
________________________________________
Author of the notes: Antonio J. Pan-Collantes
INDEX: